CORRECTION ~Epreuve N°1 : Algorithmes et Structures de Données
• Question 1 – Connaissances générales : 4 points
• Question 2 – Tas : 1.5 points
• Question 3 – Arbre AVL : 1.5 points
• Question 4 – Utilisation des structures de données : 4 points
• Question 5 – Ecriture de fonction sur les arbres : 2 Points
• Question 6 – Ecriture de fonction sur les piles : 2 Points
• Question 7 – Listes et arbres binaires: 6 points
Question 1. Cochez les affirmations qui sont correctes :
Le temps d’accès au dernier élément d’une liste simplement chainée est en O(n).
ˇ Dans un arbre binaire de recherche le minimum est toujours à la racine de l’arbre.
ˇ Le temps d’accès à l’élément maximum d’un tas min est en O(1).
ˇ Un arbre AVL est un tas.
Pour un arbre binaire de recherche donné l’obtention de la liste des nombres triés est en temps O(n).
ˇ Dans un tas, la primitive supprimerValeur consiste à supprimer une valeur située dans une feuille.
La complexité mémoire d’une table de hachage chainée est plus importante que la complexité mémoire
d’une table de hachage ouvert
ˇ Si s est une variable de type ^entier, on modifie la valeur de l’entier en écrivant s=s+1
Question 2. Soit la suite de clé 5,8,2,6,3,4,1,7. Construire le tas-Min correspondant à l’insertion
consécutive des clés, on dessinera l’arbre après chacune des quatre premières insertions ainsi que l’arbre
final. Montrez l’exécution de supprimerValeur sur le tas ainsi construit.
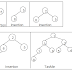
Question 3. On donne l’arbre AVL suivant.
1 – Donnez sur l’arbre ci-dessus les positions des insertions de feuille qui conduiront à un arbre
déséquilibré ?
2 - Donnez sur le dessin les facteurs d’équilibrage.
3 - Dessinez et expliquez les modifications de l’arbre lors de l’insertion de la valeur 65. On mentionnera
les modifications des facteurs d’équilibrages.
La valeur 65 s’insère comme fils gauche du noeud contenant 70. Par suite, l’arbre est déséquilibré. Le
facteur d’équilibrage du noeud contenant 70 passe à -1, celui correspondant à 80 passe à -1. Le noeud
pour lequel le facteur de déséquilibrage est mauvais est le noeud contenant la valeur 100
(facteur d’équilibrage -2). On effectue donc une rotation à droite autour du noeud 100. Après cette
opération l’arbre est AVL.
Question 4. Un dispositif dispose de deux robots pour traiter des commandes. Une commande est
identifiée par un nom sur 30 caractères et un date sous la forme [jour,mois,année]. Le premier robot (R1)
mémorise les commandes dès quelles lui parviennent. Le second robot (R2) traite les commandes.
1 – Quelle structure de données pertinente peut-on utiliser pour accéder en temps constant aux
identificateurs des commandes ?
Une table de hachage, il suffit d’écrire une fonction qui transforme le libellé de la commande en un entier
qui sera ensuite haché. On peut définir une fonction commandeToEntier qui prend en argument une
commande et la transforme en entier.
2 – Quelle structure de données peut utiliser R1 pour que R2 traite les commandes dans le même ordre où
elles arrivent à R1 ?
Une file : le premier entré dans la file est le premier traité.
3 – Décrivez le type de cette structure et notamment on détaillera les éléments de la structure.
Type FC : file de entier ;/* on stocke les valeurs de hachage*/
L’entier dans la structure est une valeur de hachage de l’élément de commande.
Commande=structure
Code :entier ; /* obtenu par la fonction commandeToEntier */
Nom :tableau[1..30] de char ;
Date :structure
Jour :entier ;
Mois :entier ;
Année : entier ;
Finstructure
finstructure
Si on choisit un adressage ouvert on a donc une table de hachage de Commande. Si C est une commande
la clé doit être calculée à partir de C.code. Il faut donc modifier les fonctions de hachage.
4 – Ecrire les fonctions ajouterCommande (utilisée par R1)et supprimerCommande utilisé par R2.
Fonction ajouterCommande(ref F :FC ; ref T : tableHash de commande ;ref C :commande) :vide
Début
Enfiler(F,ajouter(C,T))
Fin
Fonction supprimerCommande(ref F :FC ; ref T : tableHash de commande) :vide
Début
Supprimer(valeur(F),T) ;
Défiler(F)
Finsi
5 – Modifier la fonction ajouterCommande pour éviter les doublons.
Fonction ajouterCommande(ref F :FC ; ref T : tableHash de commande ;ref C :commande) :vide
Début
Si chercher(T,C)==NIL alors
Enfiler(F,ajouter(C,T))
finsi
Fin
4/10
Question 5. On définit la longueur de cheminement externe d’un arbre binaire comme la somme des
hauteurs des feuilles (nombre d’arêtes de la racine à la feuille). Ecrire la fonction longueurDeCheminement qui
prend en paramètre un arbre et calcule se paramètre.
Fonction longueurDeCheminement(ref A :arbreBInaire ;val h :entier) :entier
Début
Si estFeuille(A) alors
retourner(h)
sinon
c=0 ;
si filsGauche(A) !=NIL alors
c=c+ longueurCheminement(filsGauche(A),h+1)
finsi
si filsDroit(A) !=NIL alors
c=c+ longueurCheminement(filsDroit(A),h+1)
finsi
retourner( c)
fin
L’appel se fait avec longueurCheminement(A,0).
Question 6. Ecrire une fonction sup3 qui prend en entrée une pile d’entier et qui fournit en sortie la pile
modifiée telle que tous les nombres multiples de 3 se retrouvent en tête de pile et dans le même ordre que
la pile. Par exemple, [1,3,5,4,2,6,8 est transformée en [1,5,4,2,8,3,6.
Fonction sup3(ref P :pile d’entier ) :vide
Var PC,P3 :pile d’entier ;
Var v :entier ;
Début
creerPile(PC) ;
creerPile(P3) ;
tantque !pileVide(P) faire
v=valeurPile(P) ;
depiler(P) ;
si v est multiple de 3 alors
empiler(P3,v)
sinon
empiler(PC,v)
finsi
fintantque
copierPile(PC,P) ;
copierPile(P3,P) ;
fin
fonction copier(ref P1,P2 :pile d’entier) :vide ;
début
tantque !pileVide(P1) faire
empiler(P2,valeurPile(P1)) ;
dépiler(P1) ;
fintantque
fin
5/10
Question 7. On considère un tableau de dimension N contenant des entiers tous différents appartenant à
l’intervalle [1..N]. Par exemple, le tableau de dimension 8 contient 5,8,2,6,3,4,1,7.
1 – Ecrire une fonction tableauToListe qui transforme un tableau en une liste simplement chainée en
conservant l’ordre des entiers dans le tableau et renvoie vrai si les éléments du tableau sont conforme à
l’énoncé (des entiers tous différents) et faux sinon.
On écrit d’abord une fonction de vérification de la contrainte. En effet, si la vérification se fait en cours
de construction de la liste, il faudra en cas de viol de la condition détruire la liste ce qui est coûteux en
temps et en mémoire.
Fonction vérifier(ref T :tableau[1..N] d’entiers) :booléen ;
Var i :entier ;
Var B :tableau[1..N]de booleen ;
Début
Pour i allant de 1 à N faire
B[i]=faux
Finpour
Pour i allant de 1 à N faire
Si B[T[i]]==vrai alors
retourner(faux)
sinon
B[T[i]]=vrai
Finsi
Finpour
Retourner(vrai)
Fin
fonction tableauToListe(ref L :listed’entier ;refT :tableau[1..N]d’entier) :booleen ;
/* on suppose que la liste n’est pas créée*/
Var P :^cellule ;
Début
Si !verifier(T) alors
Retourner(faux)
Sinon
creerListe(L) ;
insererEnTete(T[1],L) ;
P=premier(L) ;
Pour i allant de 2 à N faire
insererApres(T[i],L,P) ;
P=suivant(L,P) ;
Finpour
Retourner(vrai)
Finsi
Fin
2 – Ecrire une fonction picDeListeSC qui à partir de la liste ainsi constituée fournit la liste des valeurs T[j]
telles que T[j-1]<T[j] et T[j]>T[j+1] (sur l’exemple (4,6,8)).
fonction picDeListeSC(ref L :listeSC d’entier) :listeSC d’entier;
Var SSP,P :^cellule ;
Var pic :listeSC d’entier ;
Début
creerListe(pic) ;
P=premier(L) ;
Si ! listeVide(L) et suivant(L,P) !=NIL alors
SP=suivant(L,P)
SSP=suivant(L,SP) ;
6/10
Tantque SSP !=NIL faire
Si contenu(SP)>contenu(P) et contenu(SP)>contenu(SSP) alors
insererEnTete(contenu(SP),pic)
finsi
P=SP ;
SP=SSP ;
SSP=suivant(L,SP)
Fintantque
Finsi
Retourner(pic)
Fin
3 – Si on choisit d’utiliser des listes doublement chainées, écrire la fonction picDeListeDC en utilisant la
primitive précédent.
fonction picDeListeDC(ref L :listeDC d’entier) :listeSC d’entier;
Var ,P :^cellule ;
Var pic :listeSC d’entier ;
Début
creerListe(pic) ;
P=premier(L) ;
Si ! listeVide(L) et suivant(L,P) !=NIL alors
P=suivant(L,P)
Tantque suivant(L,P) !=NIL faire
Si contenu(P)>contenu(suivant(L,P) et contenu(P)>contenu(precedent(L,P)) alors
insererEnTete(contenu(P),pic)
finsi
P=suivant(L,P)
Fintantque
Finsi
Retourner(pic)
Fin
4 – Donnez les avantages et les inconvénients des deux implémentations et des deux fonctions :
• En temps
Les deux fonctions sont équivalentes en temps : une boucle tantque qui parcours une liste de taille N.
• En mémoire
Les deux fonctions ne sont équivalentes la fonction en listeSC utilise moins de mémoire par définition que
celle en listeDC puisque une cellule stocke un pointeur de plus. Cependant en ce qui concerne la
complexité, elles sont équivalentes, O(n).
• En lisibilité de la fonction.
Il y a un avantage léger pour la fonction listeDC. En effet, au niveau du test on comprend mieux les
comparaisons qui sont effectuées grâce à la primitive precedent.
5 – Ecrire une fonction tableauToABR qui transforme un tableau en un arbre binaire de recherche renvoie
vrai si tous les éléments du tableau sont conformes à l’énoncé (des entiers tous différents) et faux sinon.
On donnera l’algorithme COMPLET d’insertion.
fonction insertion(ref x:^sommet, val e:entier):vide;
var s:^sommet;
début
si valeurSommet(x)>e alors
s=filsGauche(x);
si s==NIL alors
ajouterFilsGauche(x,e);
sinon
insertion(s,e);
finsi
sinon
s=filsDroit(x);
7/10
si s==NIL alors
ajouterFilsDroit(x,e);
sinon
insertion(s,e);
finsi
finsi
fin
finfonction
fonction tableauToABR(ref A :arbreBinaire d’entier ;refT :tableau[1..N]d’entier) :booleen ;
/* on suppose que l’arbre n’est pas créée*/
Début
Si ! verifier(T) alors
Retourner(faux)
Sinon
creerArbre(A,T[1]) ;
Pour i allant de 2 à N faire
insertion(racine(A),T[i]) ;
Finpour
Retourner(vrai)
Finsi
Fin
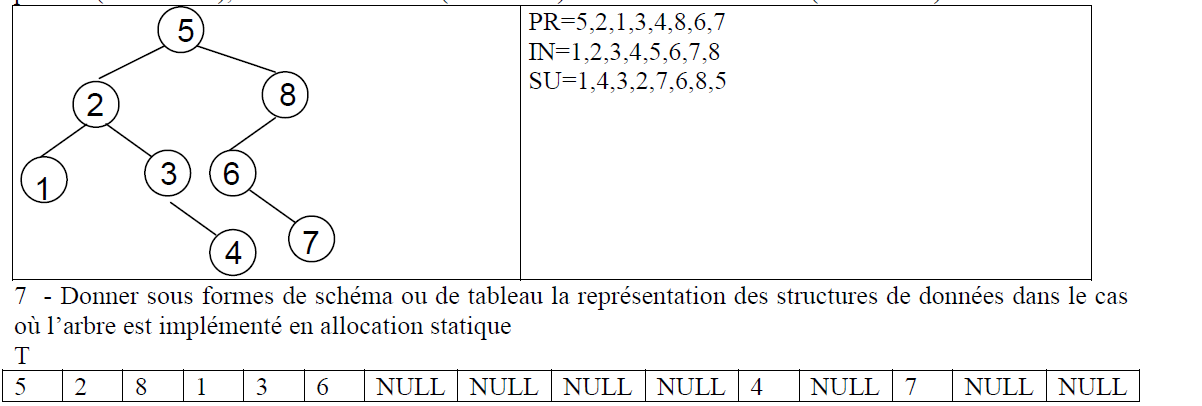
6 – Appliquer cette fonction au tableau donné en exemple. Donnez la suite des valeurs dans l’ordre
préfixe (tableau PR), dans l’ordre infixe (tableau IN) et dans l’ordre suffixe (tableau SU).
8 - Donner sous formes de schéma ou de tableau la représentation des structures de données dans le cas
où l’arbre est implémenté en allocation dynamique
FIN









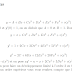






0 commentaires: